Что такое призма — определение и разновидности призм

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем о такой интересной геометрической фигуре, как ПРИЗМА.

Школьники сталкиваются с ней на уроках геометрии только в 10 классе. Соответственно, те, кто решил уйти после 9-го класса в колледж, этих знаний лишены. И мы восполним этот пробел.

А старшеклассникам наша статья (очень на это надеемся) поможет при подготовке к сдаче ЕГЭ. На экзаменах по математике попадаются несколько вопросов, связанных с ПРИЗМАМИ.

Призма – это ...

Призма – это геометрическая фигура, которая представляет собой объемный многогранник. Две его стороны лежат на параллельных основаниях и представляют собой различные многоугольники. А боковые грани – это параллелограммы, которые соединяются с основаниями.

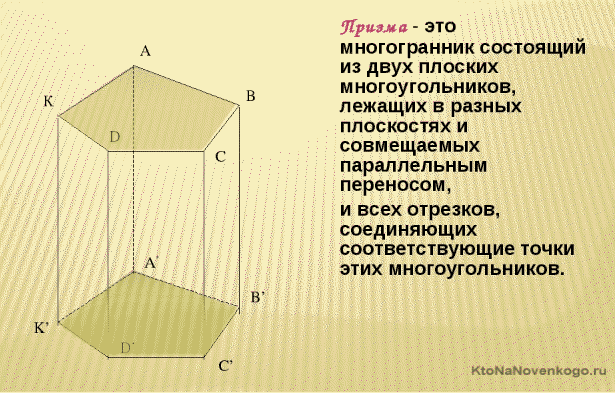
Выглядит классическая призма так, как показано на рисунке выше.

На этом рисунке четко видны все элементы призмы:

1. Основание – два многоугольника, которые параллельны друг другу;
2. Боковые грани – четырехугольники, которые скрепляют оба основания и имеют с ними одинаковые грани.

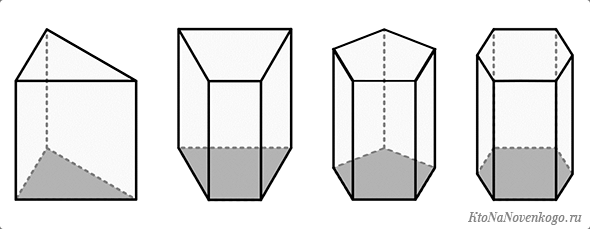
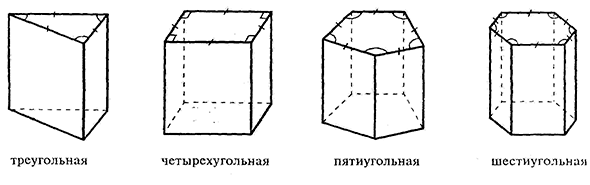
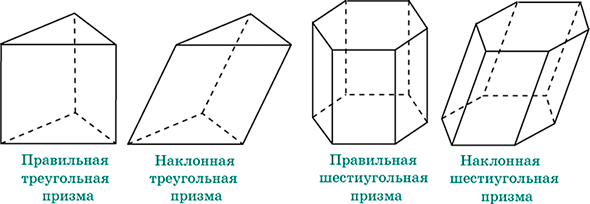
В зависимости от вида основания призмы бывают:

1. Треугольные – в основаниях находятся два треугольника.
   
2. Четырехугольная призма – в основаниях различные четырехугольники. В том числе прямоугольник, квадрат или параллелограмм.
   
3. Пятиугольная призма – в основании лежит пятиугольник. Называют часто пентапризмой. А если пятиугольник правильный – то усеченным осоэдром.
   
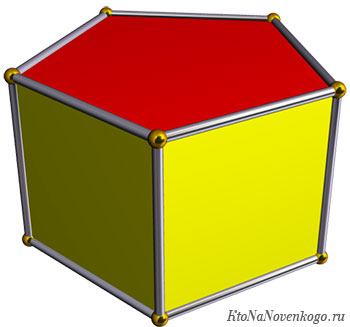
4. Шестиугольная призма – в основании, как нетрудно догадаться, находится шестиугольник. Если фигура правильная, то ее часто называют усеченным шестигранным осоэдром. Кстати, именно такая форма у многих карандашей – до затачивания, конечно.
   
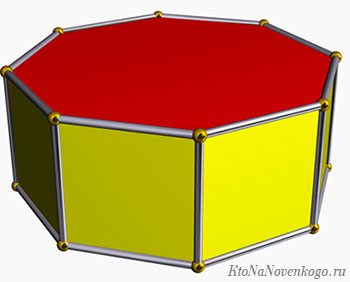
5. Восьмиугольная призма – фигура, которая называется зоноэдр.
   

Разнообразие призм можно считать бесконечным. Могут быть фигуры, у которых в основании и 10-угольник, и 20-угольник, и даже 100-угольник. Но, к счастью, такие фигуры попадаются крайне редко. И их точно не изучают в школе.

История изучения призмы

О существовании призм знали еще в Древнем Египте и Древнем Вавилоне. Об этом свидетельствуют различные археологические находки, прежде всего, остатки зданий и памятников.

Но научное описание призм – это заслуга древнегреческих математиков. В первую очередь, Аристотеля. Он даже целое направление науки придумал – стереометрией. В переводе с греческого это означает измерение пространства («метрио» — измерение, «стереос» — пространство).

И в рамках этой науки Аристотель занимался изучением призм, кубов, параллелепипедов и других объемных геометрических фигур.

Естественно, не обошел своим вниманием призмы и знаменитый древнегреческий математик и ученый – Евклид. В своих трудах он дает следующее описание:

Призма – это телесная (то есть пространственная) фигура, которая заключена между несколькими плоскостями. Две из них параллельны друг другу, равны и противоположны. А другие в любом количестве представляют собой параллелограммы.

Кстати, само слово «призма» также имеет древнегреческие корни. И означает оно «πρίσμα» — отпиленное. И действительно, внешне призма напоминает фигуру, которую взяли и вырезали из чего-то более длинного. Как будто ствол дерева распили на несколько поленьев.

Элементы призмы

Рассмотрим для примера такую вот призму.

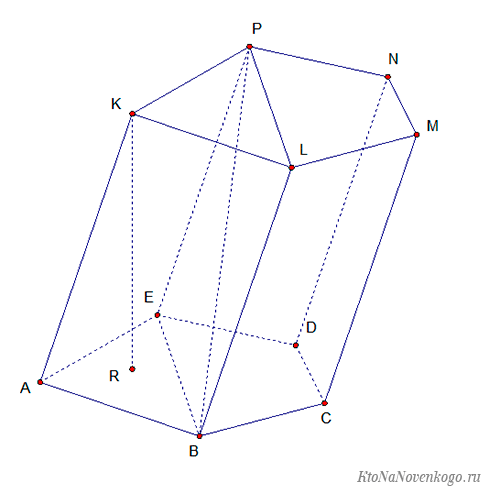
Она пятиугольная и состоит из следующих элементов:

1. Основание – их, как и положено, две штуки, в данном случае это пятиугольники ABCDE и KLMNP;
2. Боковая грань – их количество равно количеству углов оснований, то есть тоже пять. Это параллелограммы ABKL, BCLM, CDMN, DENP и EAPK;
3. Боковая поверхность – так называют сумму всех имеющихся боковых граней, которые мы перечислили выше;
4. Полная поверхность – это сумма всех частей призмы;
5. Боковое ребро – линии соединения боковых граней. В нашем случае это отрезки KA, LB, MC, ND и PE;
6. Высота – отрезок, который соединяет основания призмы под прямым углом. В нашем случае KR. Это касается наклонных призм, у которых грани не перпендикулярны основаниям. В противном случае, высота совпадает с боковым ребром;
7. Диагональ – отрезок (PВ), который соединяет две вершины призмы, не относящиеся к одной грани;
8. Диагональная плоскость – плоскость, которая проходит через основание, боковую грань и диагональ. В нашем случае это BPE и BPL;
9. Диагональное сечение – плоскость, которая образуется пересечением призмы и диагональной плоскостью. В нашем случае это параллелограмм BLPE. В частных случаях она может быть ромбом или квадратом.

Подобные элементы есть у каждой призмы, независимо от ее вида.

Разновидности призм

Все призмы можно поделить на три категории:

1. Прямая призма – эта такая геометрическая фигура, у которой боковые грани соединяются с основаниями под прямым углом. Соответственно, они являются прямоугольниками. А саму призму часто еще называют прямоугольным параллелепипедом.
   
2. Правильная призма – эта геометрическая фигура, у которой в качестве оснований используются правильные многоугольники. То есть те, у которых все стороны равны между собой. А боковые грани у таких призм также идентичны друг другу.
   
3. Наклонные призмы – геометрические фигуры, у которых боковые ребра не пересекаются с основанием под прямым углом. Именно у таких призм появляется такой элемент, как высота.
   

Вместо заключения

Слово ПРИЗМА используется не только в геометрии, хотя именно это значение считается главным. И именно оно первым записано во многих словарях. Но есть и другие варианты:

1. Физика – устройство для преломления световых лучей.
2. Риторика – оценка с учетом определенных факторов. Например, «Он смотрел на нее через призму прожитых лет» или «Он общался с ними через призму своего настроения».
3. Техника – элемент металлорежущего станка, который предназначен для закрепления на нем цилиндрической заготовки.

А еще «Призма» — это кодовое название советской радиостанции 5-АК. Есть такой хоккейный клуб в Латвии – «Призма-Рига». И наконец, в Финляндии существует сеть продуктовых магазинов «PRISMA».