Периметр прямоугольника

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем, что такое периметр прямоугольника и по каким формулам его можно посчитать.

Тема в общем-то простая, каждый из нас изучал ее еще в начальных классах. Тем не менее с возрастом кто-то мог что-нибудь и подзабыть.

Но для начала предлагаем освежить теоретическую базу и вспомнить, что такое прямоугольник.

Что такое прямоугольник и что такое периметр

Прямоугольник – это геометрическая фигура, которая представляет собой четырехугольник, а конкретно параллелограмм (фигура, у которой противоположные стороны равны и параллельны). Но параллелограмм не обычный, а с особенностями. У него все стороны пересекаются друг с другом под прямым углом.

Выглядит прямоугольник соответственно:

А частным случаем прямоугольника является квадрат:

У такого прямоугольника стороны не только пересекаются под прямым углом, но и равны между собой.

Как и многие термины в математике, жир слово пришло к нам из Древней Греции. Дословно оно означает «περιμετρέο» — «окружность» или «измерять вокруг». Таким образом,

Периметр – это совокупная длина границ любой геометрической фигуры. Этим словом обозначают как сами границы, так и их математическое значение.

С этим словом мы часто встречаемся в повседневной жизни. Например, когда нужно поставить забор на дачном участке, то его устанавливают по периметру участка. И мы понимаем, что речь идет о границах.

Также, солдаты или полицейские часто стоят в оцеплении «по периметру» какой-то территории. А кулинары часто украшают торт фруктами или кремовыми цветами также «по периметру».

Как найти периметр прямоугольника

Возьмем для примера такой прямоугольник:

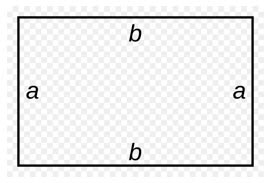
Исходя из общего определения, чтобы посчитать периметр прямоугольника, надо просто сложить все его стороны.

Периметр в математике обозначается латинской буквой «Р». И соответственно формула выглядит так:

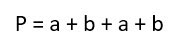
С учетом равенства сторон, формулы можно существенно упростить:

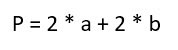
или

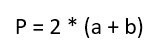
Предположим, что у нас длина прямоугольника равна 4 сантиметрам, а ширина 2. Тогда периметр этой геометрической фигуры составит:

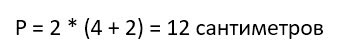
И тут появляется важное замечание. Периметр измеряется в тех же величинах, что и длины сторон прямоугольника. Это могут быть миллиметры, сантиметры, метры, километры и так далее.

В случае с квадратом, который, напомним, является частным случаем прямоугольника, посчитать периметр еще проще. Благодаря тому, что у него все стороны равны (назовем их условно «а»), формула выглядит так:

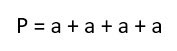
или

Опять же приведем конкретный пример. Если возьмем квадрат со стороной 4 сантиметра, то его периметр составит P = 4 * 4 = 16 сантиметров.

Другие формулы для расчета периметра прямоугольника

Иногда школьникам предлагают такую задачу – нужно вычислить периметр прямоугольника, зная его площадь и длину одной стороны.

Тут надо знать, как вычисляется сама площадь. Для этого надо просто перемножить длины двух сторон:

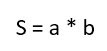
Соответственно, мы можем определить длину недостающей нам стороны. Для этого надо просто разделить площадь на другую сторону:

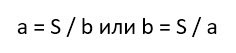
Таким образом, мы у нас будут значения обеих сторон прямоугольника. А уже после периметр вычисляется по стандартной формуле.

Вместо заключения

Зная длины сторон, можно вычислять и периметры более сложных прямоугольных фигур. Вот таких:

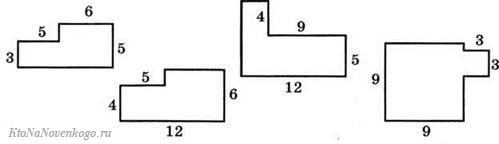
Страшно выглядят они только на первый взгляд. А на деле, надо просто провести недостающую линию и разделить каждую из фигур на два прямоугольника. Далее вычисляем их по отдельности и складываем друг с другом. Как результат – общий периметр фигуры.

Вот и все, что мы хотели сегодня рассказать.