Ромб – между параллелограммом и квадратом
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем о такой геометрической фигуре, как РОМБ. Многие наверняка знают, как он выглядит.
Особенно спортивные болельщики, так как эмблемы многих команд связаны именно с ромбом. Тут достаточно вспомнить одну из главных российских команд – Спартак. Вот так она выглядит.

Ромб — это...
А вот как звучит официальное определение ромба:
Ромб – это геометрическая фигура, которая представляет собой особый вид параллелограмма. И у него все стороны равны.
История возникновения самого слова весьма примечательна. На древнегреческом оно звучит как «ῥόμβος», а на латыни «rombus». И переводятся оба слова как «бубен».
Дело в том, что в Древней Греции делали барабаны и прочие ударные инструменты чаще именно такой формы. Просто натягивать ткань на параллелограмм было гораздо проще. А вот круглые, более привычные нам сегодня барабаны появились позже.
И еще один интересный факт – карточная масть «бубны» называется так точно по той же причине.

Говоря об определении РОМБА, не лишним будет тогда сказать и что такое параллелограмм, раз он там фигурирует.
Параллелограмм – это геометрическая фигура, которая представляет собой четырехугольник, у которого противоположные стороны равны между собой и параллельны друг другу.
Выглядит классический параллелограмм вот так:
Впервые его описал знаменитый древнегреческий математик Евклид в своей книге «Начала». Это произведение вышло в 300 году до нашей эры. И было посвящено основам математики, которые были известны на то время.
В частности, Евклид в своей книге разделил все четырехугольники на две большие категории – параллелограмм и трапеция (так как у нее две стороны не параллельны друг другу). Также в «Началах» Евклид указал, что ромб является частным случаем параллелограмма, так как у него противоположные стороны равны.
И наконец, частным случаем самого ромба является квадрат. У него противоположные стороны не только равны, но еще и пересекаются под прямым углом.

Признаки ромба
Чтобы понять, что перед нами ромб, должно выполняться всего лишь одно из трех простых условий:
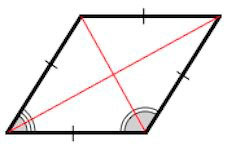
- Все четыре стороны параллелограмма равны;
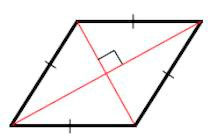
- Диагонали параллелограмма пересекаются под углом 90 градусов;
- Диагонали параллелограмма являются еще и биссектрисами.
И тут будет не лишним подтянуть теоретическую базу и напомнить, что такое диагональ, и уж тем более что такое биссектриса.
Диагональ – это отрезок, который соединяет две любые вершины в многоугольнике, которые не находятся рядом друг с другом.
Если говорить конкретно о четырехугольнике, которым является и ромб, то диагональ соединяет две противоположные вершины и никак иначе. И таких диагоналей в ромбе две:
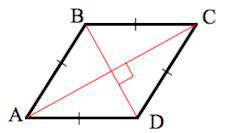
На этом рисунке диагоналями являются отрезки AC и BD. И как показано, они пересекаются под прямым углом, о чем и говорится во втором признаке ромба.
Биссектриса – это линия, которая выходит из угла и делит его ровно на две части.
Кстати, само слово «биссектриса» имеет латинские корни. Оно состоит из двух половин – «bi» (двойное) и sectio (разрезание).
Свойства ромба
А можно все и перевернуть таким образом. Если вы точно определи, что перед вами ромб, то тогда для этой фигуры будут характерны вот такие свойства:
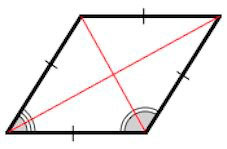
- Диагонали ромба пересекаются между собой под прямым углом.
- Диагонали ромба также представляют собой и биссектрисы его углов.
И есть еще одно свойство, которое помогает решать различные задачки на уроках геометрии. Оно звучит так:
Сумма квадратов обеих диагоналей ромба равна квадрату его сторону, умноженному на четыре.
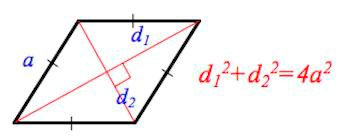
Периметр ромба
Чтобы определить периметр любого четырехугольника, надо просто сложить между собой длины всех его сторон.
В случае с ромбом это совсем просто, так как они все равны между собой. И тогда формула для вычисления периметра получается такой:
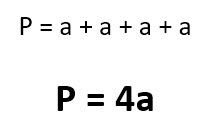
Как несложно догадаться, буква «а» здесь – это длина стороны ромба.
Есть еще одна формула для вычисления периметра ромба – через диагонали. Она более сложная, но при решении различных задач вполне может и пригодиться.
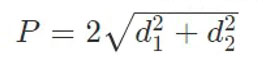
Площадь ромба
Площадь любой геометрической фигуры – это размер пространства, заключенного в границы этой самой фигуры.
Классическая формула для расчета площади ромба – через длины стороны и высоты.
Главное, надо напомнить, что такое высота. Это отрезок, проведенный из вершины геометрической фигуры под прямым углом к противоположной стороне.
Она обозначается буквой «h» или «H» и выглядит вот так:
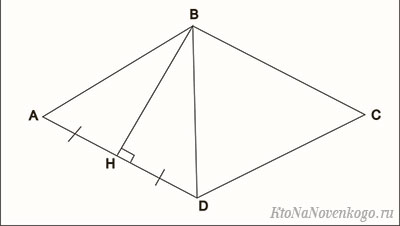
И наконец, формула для расчета площади ромба через сторону и высоту:
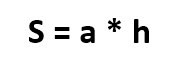
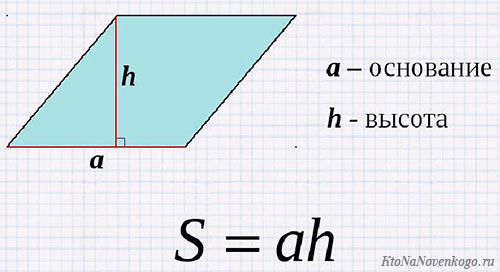
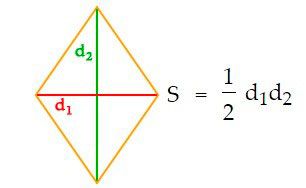
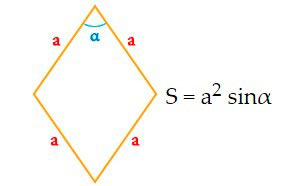
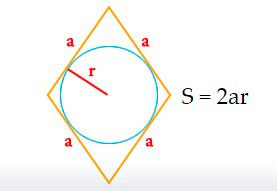
Есть и другие формулы для расчета площади ромба:
- Если известны диагонали:
- Если известны сторона и угол:
- Если известны угол и радиус вписанной окружности:
- Если известны сторона и радиус вписанной окружности:
Вот и все, что мы хотели рассказать о ромбе.
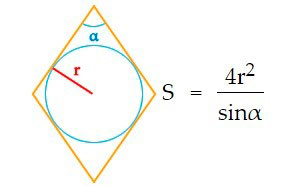
Комментарии и отзывы (1)
Со временем, разница между квадратом, ромбом и параллелограммом забывается. То, что было само собой разумеющимся в школе, теперь кажется чем-то новым!:) Кстати, во времена СССР, именно ромб был самой популярной фигурой в дизайне всевозможных логотипов.
Ваш комментарий или отзыв