Что такое сложные проценты — определение и как они влияют на доход
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Даже если вы никогда ничто и никуда не инвестировали, то наверняка все же сталкивались с таким понятием, как сложный процент.
Чаще всего это происходит, когда вы открываете депозит в банке и у вас интересуются, хотите ли вы открыть вклад «с капитализацией» или «без».

Вариант «с капитализацией» как раз и является использованием сложных процентов при подсчете ваших доходов.
Но это понятие также активно используется в области инвестиций, да и вообще в любых областях бизнеса и финансов. Поэтому важно понимать, что это такое и как может отразиться на ваших доходах.
Определение термина сложный процент — что это
Сложные проценты – емкий термин, которым привыкли оперировать инвесторы, финансисты, бизнесмены. Под это определение попадает сразу несколько понятий.
Если рассматривать сложные проценты по вкладу, то это добавление к его сумме уже начисленных процентов (например, ежемесячно).
Это также и реинвестиции дивидендов владельцами ценных бумаг, с целью увеличения начального капитала.
Сложные проценты — это также и увеличение вложений в новые проекты . Их владелец бизнеса делает за счёт той прибыли, что он получает сейчас от бизнес-деятельности.
Проще всего понять, что такое сложный процент, на конкретном примере. Допустим, участник валютного рынка внес на ПАММ счёт 1000 долларов с учётом того, что ежемесячный процент прибыли составляет 6%.
Если он эту прибыль будет ежемесячно забирать со счёта, то через три года она составит 216%. Это обычный простой процент.
А если он будет всю полученную прибыль снова пускать в дело, присоединяя её к основному счёту, то через три года он получит уже более 800%.
С помощью продуманного реинвестирования, к которому добавлялись кредиты и маржинальные займы, смогли сформировать свои огромные состояния такие известные финансисты, как семейство Ротшильдов. Уильям Баффетт, Джордж Сорос.
Все они отлично знали, как используются сложные проценты в инвестировании.
Риск и выгода реинвестиций
Критики применения реинвестиций и применения сложных процентов апеллируют к их высокой рискованности.
Действительно, компания может в короткий срок стать банкротом, инвестиционный сайт просто зарыться, а управляющий трейдер сделать глобальную ошибку и потерять деньги клиентов.
Исходя из таких вероятностей, критики не рекомендуют полностью инвестировать прибыль, ссылаясь на то, что «класть все яйца в одну авоську» не следует, и лучше полученную прибыль вложить в другой перспективный проект, или же просто вывести из оборота и использовать по другому назначению.
С какой-то стороны критики правы: не очень надежных компаний много, да и мировые рынки отнюдь не настолько стабильны, насколько нам бы хотелось.
Однако 800% за три года – слишком впечатляющая величина, чтобы относиться к сложным процентам недостаточно уважительно. А если рассчитывать сложные проценты не на три года, а, допустим, на 50 лет?
Вот ещё один простой пример.
Мы кладём 1000 рублей на депозит в солидном банке под 12% годовых, и получаем по прошествии года уже 1120 рублей. На следующий год наш вклад будет уже не 1000, а целых 1120 за счёт капитализации — присоединения полученных процентов к основному счёту.
Пройдёт ещё год, и прибыль составит не 120 руб. как за первый год, а уже 134,4 рубля. Казалось бы, не так уж и велика разница. Но пройдёт 10 лет, и сумма прибыли составит уже 3100 рублей, через 20 лет она будет равна 9640 рублей, а через 50 лет — 289 000 рублей.
Если с простыми процентами прибыль растёт линейно, то в соответствии с формулой сложных процентов, реинвестиции увеличивают капитал по экспоненте.
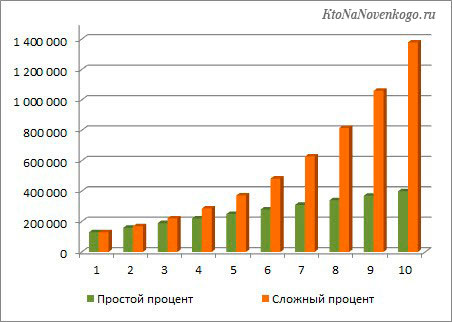
Чем больший размер был у начального капитала и чем дольше мы оставляли его на депозите, тем интенсивнее его рост, причём ускорение будет только возрастать.
Формула сложных процентов
Для расчёта экспоненциальной функции существует формула:
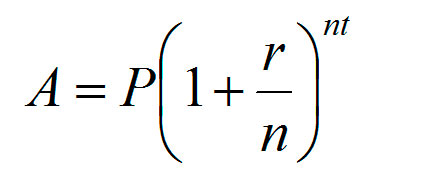
- А – это сумма, которая в результате окажется на счёте.
- Р – начальная сумма, которую мы инвестировали, или внесли на депозит.
- r – процентная ставка (годовая)
- n – количество раз за год, когда учитывается процентная ставка (бывает, что её учитывают раз в месяц, раз в квартал, или в год. Это указывается в любом договоре).
- t – число лет, через которые мы ждём результат.
Когда на счету будет миллион
Но, есть определённая сложность.
Чтобы сложные проценты смогли показать всё, на что они могут быть способны, требуется продолжительное время. Или же процентная ставка должна быть высокой, что случается очень редко в проектах, где не замешано мошенничество.
Считается, что о сложных проектах любил размышлять Альберт Эйнштейн, считая их великим изобретением. По крайней мере, так говорится в разнообразной мотивационной литературе.
В ней также любят использовать такой пример:
Если внести на депозит всего один доллар под 20% годовых со сложным процентом, а затем каждый день докладывать к ним ещё по одному, то пройдёт всего каких-нибудь 32 года, и формула сложных процентов принесёт миллион.
Звучит красиво, и нельзя сказать, что это неправда.
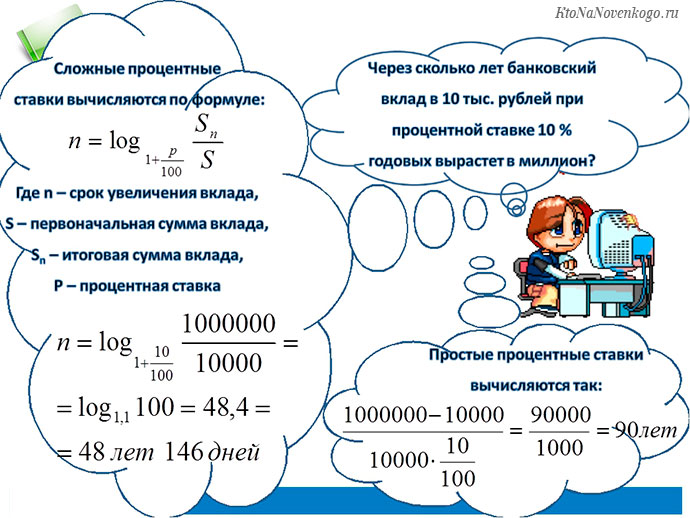
Однако 20% годовых сегодня могут предложить только те, кто задумал обман, то есть, мошенники. Банки в России сегодня готовы предложить вкладчикам не более 4% годовых, следовательно, миллион таким способом накопится только через 120 лет. Что, конечно, тоже неплохо.
Комментарии и отзывы (2)
По теории все правильно, но где взять такие предложения на рынке? Сейчас депозиты, в большинстве своем, без капитализации, да и нет вкладов со сроком в несколько лет, обычный срок до года включительно. Поэтому нужно смотреть реально на вещи, а не витать в облаках.
Это где нет вкладов с капитализацией и ограничения до года? Вы страну-то уточните. В России с этим все как было, так и есть — нормально. Другое дело, что проценты уже не слишком вкусные, но зато кредиты более доступны стали. Либо, либо...
Ваш комментарий или отзыв