Что такое постулат — определение (просто о сложном), значение, источники и примеры постулатов

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Некоторые термины будто созданы, чтобы пугать людей. Слово «постулат» как раз такое.

Сразу же представляется грозное нагромождение формул на доске университетского профессора. На самом деле, все намного проще. Дочитав статью до последней точки, вы в этом убедитесь.

Определение понятия Постулат – что это?

Термин образовался от латинского слова postulatum, что переводится как «требование». Словарь Ожегова дает такое определение:

«Постулат – это исходное положение, допущение, принимаемое без доказательств, аксиома».

Считается, что «аксиома» – это синоним слова «постулат». Споры по этому поводу не утихают до сих пор. Есть альтернативная точка зрения, по которой:

аксиома – это утверждение, обладающее самоочевидностью (например: «часть всегда будет меньше целого»), а постулат – это просто допущение.

Мы не будем ввязываться в войну формулировок: разница между терминами настолько легка и неуловима, что ей можно пренебречь. Даже в кругу научных светил вас вряд ли поднимут на смех, если назвать аксиомы постулатами или наоборот.

Постулировать – это значит без доказательства принимать утверждение в качестве исходного положения для данной теории.

Значение постулатов для научного познания

Постулат – это основа для теории.

Если мы возводим дом, то начинаем с фундамента. От него зависит, насколько устойчивой получится конструкция. Вот и для научной теории необходим надежный фундамент – факты, на которые можно опираться, использовать для построения выводов.

Без постулатов было бы невозможно что-либо доказать. Пришлось бы ставить под сомнение исходное утверждение, потом исходное утверждение исходного утверждения... и так по цепочке в бесконечную последовательность доказательств.

Еще постулат может формулировать правила вывода – способ, по которому нужно переходить от предпосылок к следствиям из них. Например, Шерлок Холмс руководствовался принципом: идти от частного к общему (индуктивный метод мышления, хотя ему приписывали дедуктивный). Видя мелкие детали на часах собеседника, он мог рассказать историю жизни их владельца.

Откуда они берутся

1. Рождаются из опыта, экспериментов и наблюдений.
2. Заимствуются из религиозных представлений.
3. Выводятся из философской картины мира.
4. Принимаются условно (конвенционально), как приемлемое упрощение.

Примеры постулатов

Утверждения, принимаемые без доказательств, используются в логике, математике, философии, физике и других науках. Выражение используют в повседневной речи для придания словам значимости.

Постулаты в философии

Немецкий философ Кант установил постулаты практического разума – допущения, которые не доказаны, но достоверны с высокой степенью вероятности. Таких утверждений ровно три:

1. свобода воли;
2. душа бессмертна;
3. Бог — существует.

Кант не настаивал на абсолютной истинности этих идей. Но он пишет о том, что в них необходимо верить, чтобы не впасть в абсурд и уныние.

Постулаты в геометрии

Впервые термин употребил древнегреческий математик Евклид в своей работе «Начала». Он привел список аксиом и постулатов, но отчего-то не стал объяснять различия между ними.

Постулаты Евклида:

1. От одной точки до другой можно провести прямую линию.
2. Отрезок можно бесконечно продолжать по прямой.
3. Любая точка может стать центром окружности.
4. Прямые углы равны друг другу.
5. Если прямая, падающая на две прямые, образует внутренние односторонние углы, в сумме меньше двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы в сумме меньше двух прямых.

Первые четыре пункта звучат очевидно и понятно даже для ребенка. А вот пятое совсем читать не хочется. Но не все так ужасно.

Последний постулат знаком любому школьнику в такой формулировке: «Параллельные прямые не сближаются, не удаляются и не пересекаются».

Сложность формулировки породила желание оспорить утверждение. Российский ученый Николай Лобачевский смог доказать, что прямые сближаются и удаляются друг от друга, если идет речь не о плоскости, а о кривой поверхности:

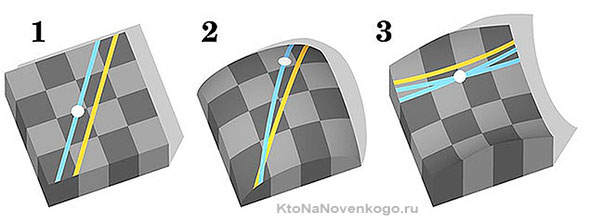
Современники не оценили заслуг Лобачевского. Его сочли не совсем адекватным человеком и отстранили от должности ректора Казанского университета. С венгерским математиком Яношем Бойяи получилось еще хуже. Во время работы над пятым постулатом бедняга сошел с ума.

Постулаты не претендуют на всеобъемлемость

Ученые не опровергают постулаты, а лишь находят границы их применения. Вот здесь это работает, а дальше – уже нет.

Лобачевский не доказал ошибочность утверждения древнегреческого математика, но указал на области, где его положение не действует.

То есть утверждение Евклида работает в рамках Евклидовой геометрии, когда речь идет о плоскости. А российского математика интересовала логика поведения прямых линий в объемном пространстве, подобном тому, где мы живем.