Что такое Логика — определение, основы, формы, законы и типы логики
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В течение дня самого обычного человека посещает тысячи мыслей. Мы думаем о реальных объектах и явлениях, о гипотетических ситуациях (кто победит, если Годзилла сразится с Кинг-Конгом?).
Но все мысли формируются одними и теми же способами по определенным принципам. Логика как раз изучает формы, методы и законы мышления.

Определение понятия — что такое логика
Этот термин имеет греческие корни. Он образовался от слова «логос», что переводится как «рассуждение, разум, мысль, смысл». Это не случайно, ведь основы современной логики заложил древнегреческий философ Аристотель.
Толковый словарь Даля дает определение: «логика — это наука здравомыслия, наука о том, как правильно рассуждать». Ее основной задачей является поиск пути перехода от предпосылок к выводу, получение достоверного знания о предмете исследования.
На самом деле, интуитивное понимание логики впитывается в нас с молоком матери. Маленький ребенок рассуждает: «Если не слушаться родителей, можно понести наказание». С детства мы учимся строить свои высказывания правильным образом, делать верные выводы, поступать логично – адекватно ситуации.

Толковый словарь Ожегова предлагает 3 значения для слова «логика»:
- наука о законах и формах мышления.
- разумность, внутренняя закономерность определенного явления или события;
- последовательность рассуждений и выводов.
Основы логики — формы логического мышления
Форма мышления – это оболочка для наших мыслей, способ по которому они строятся.
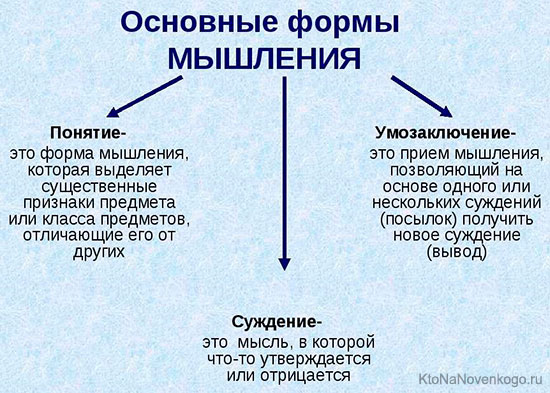
Существует всего 3 формы:
- Понятие — мысль об объекте или его свойствах. Это может быть материальный предмет (картина, растение), который можно потрогать, и что-то эфемерное (любовь, счастье), не поддающееся полному осмыслению.
- Суждение — это несколько понятий, объединенные между собой. Оно может быть либо положительным, либо отрицательным. Например, у нас есть понятия: отвага, честь, качества, главный, воин. Соберем из них суждение: отвага и честь— это главные качества воина.
- Умозаключение. Из нескольких суждений делается некий вывод, который содержит в себе новую информацию. Отвага и честь— главные качества воина. Я отважен и честен. Значит, я воин.
Все бесконечное пространство мыслей выражается этими тремя формами.
В нашей голове хранятся миллиарды понятий, которые мы объединяем в суждения, а потом делаем из них умозаключения. И все за доли секунды, даже не осознавая этого.
Законы логики (логического познания)
Законы логики — это принципы, следуя которым из истинных суждений можно гарантированно извлечь правильный вывод.
Существуют 4 закона. Порой их нарушают случайно, тогда получается ошибочное умозаключение — паралогизм. Иногда специально, с целью запутать собеседника и подвести его к ложной мысли. Тогда возникают софизмы – недостоверные выводы, которые кажутся логически правильными.
Закон тождества
Для тех, кто прогуливал в школе математику, уточню: тождество — это равенство.
Звучит закон так: понятие должно сохранять свой изначальный смысл на всем протяжении логического рассуждения.
Язык — многогранен, почти у любого слова есть несколько смыслов. Если в процессе подменить одно значение другим, получится ложный логический вывод.
Покажу на примере известной шуточной загадки: «Зачем вода в стакане?». Конечно, чтобы ее выпили. Но нет, она за стеклом. Тут как раз идет игра смыслов, нет тождества (однозначности). Понятия нельзя смешивать понятия и обязательно нужно избегать двусмысленности.
Закон непротиворечия
Два высказывания, которые несовместимы друг с другом, не могут быть одновременно истинными. Одно из них — ложное, а, возможно, и оба.
Вот Вася говорит, что Петя украл яблоко. Петя утверждает, что это сделал Вася. Эти высказывания противоречат друг другу. Значит, они не могут быть одновременно истинными. Но оба утверждения способны оказаться ложными, если есть третий вариант — на самом деле яблоко просто упало и закатилось под стол.

Логические противоречия бывают:
- контактные — высказывание подтверждается и сразу же опровергается («Я ль на свете всех милее, всех румяней и белее?» © А. С. Пушкин);
- дистантные — противоречащие друг другу утверждения разделены интервалом в речи или тексте;
- мнимые — кажется, логическая ошибка есть, но ее нет («Знаю, что ничего не знаю» © Сократ).
Контактные противоречия сразу бросаются в глаза, а вот дистантные отследить сложно. Например, неопытный оратор начинает речь с одной идеи, потом путается и в конце сам себя опровергает.
Закон исключенного третьего
Если из двух суждений одно является отрицанием другого, то они не могут быть одновременно ложными. Хотя бы одно должно быть истинным.
Этот закон тесно связан с предыдущим. Они похожи, но есть разница. Здесь рассматриваются высказывания, отрицающие друг друга («А» и «не А»), а не противоречия.
Вот пример: Вася говорит, что Петя украл яблоко. Петя утверждает, что он этого не делал. Тут нет никакого третьего варианта, одно из высказываний должно быть истинным. Это и есть пример использования закона исключенного третьего.
Закон достаточного основания
Всякое утверждение, чтобы считаться истинным и справедливым, должно быть доказано. Подтверждение можно получить эмпирическим (опытным) или теоретическим способами.
Вот ученый заявляет, что есть элементарные частицы, которые могут двигаться быстрее скорости света. Но никто не поверит, пока он не предоставит достаточно доказательств.
Основатель закона — немецкий ученый Готфрид Вильгельм Лейбниц. В повседневной жизни часто встречается нарушение этого правила.
Например, адвокат, защищая клиента, заявляет: «Мой подзащитный не мог никого убить. У него отличная характеристика с места работы. Примерный семьянин и любящий отец». Здесь аргументы совершенно не обосновывают тезис, что нарушает закон достаточного основания.
Подробнее о законах логики:
Формальная и математическая логика
Логика разделяется на 2 направления – формальное и математическое.
Формальная логика концентрируется на форме мышления, способах и методах перехода от предпосылок к правильным умозаключениям. Содержание мыслительного процесса ее не касается.
С точки зрения формальной логики, доказательство существования черных дыр ничем не отличается от обоснования необходимости взять с собой зонт в дорогу. Отцом-основателем этой ветви науки является древнегреческий мыслитель Аристотель.
Математическая логика занимается проблемой применения математических методов для решения логических задач и создания алгоритмов логического вывода.
В ней используется строгий символический язык, который позволяет уйти от проблемы нарушения закона тождества из-за ошибочного толкования отдельных терминов.
Поясним на примере:
| Символ математического языка | Значение |
|---|---|
| p | выражение «черепахи летают» |
| 0 | ложь |
| 1 | истина |
| ¬ | отрицание |
Вот так на языке математической логики можно описать выражение «черепахи могут летать»: |p|=0. А вот так выглядит фраза «черепахи не летают»: |¬p|=1.


Комментарии и отзывы (6)
Уметь мыслить логически — очень полезный навык, который сильно помогает в жизни. Жаль, что его почти не развивают в процессе обучения. Школьники и студенты просто зазубривают данные, не создавая логических связей между ними.
Значение логики сильно переоценивают. Многие гении часто принимали интуитивные и нелогичные решения, которые в последствии оказались судьбоносными. Не стоит возводить логику в культ.
Ну так черепахи летают или нет, что на сей счет думает математика? Я вот думаю, что летают, ведь если подбросить черепаху вверх, она будет лететь до тех пор пока не столкнется с Землей, а уберите силу тяжести и черепаха будет летать вечность.
Всё, что я понял из статьи, так только то, что никакого логического мышления у меня нет и никогда не было, вот так и живу, без логики.
1.Зачем вода в стакане — чтобы пить!
2. За чем вода в стакане — за стеклом!
Кто это написал?
Ваш комментарий или отзыв