Что такое катет и гипотенуза в прямоугольном треугольнике – это основы геометрии

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы подробно поговорим, что такое КАТЕТ и ГИПОТЕНУЗА. Уверены, что еще со школы все знают, что так называют стороны прямоугольного треугольника. И именно с ними связана самая знаменитая теорема в мире – теорема Пифагора.

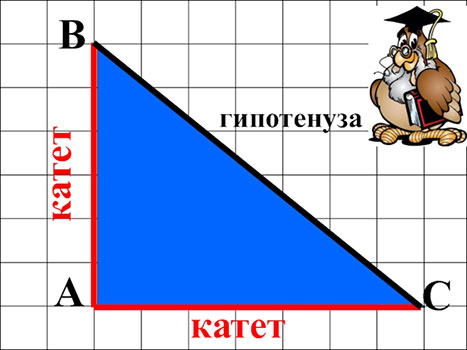
Но даже тем, у кого в школе по геометрии была твердая «пятерка», могут быть неизвестны некоторые интересные факты. А другим будет полезно освежить забытые знания.

Что такое катет

Катетом называют одну из сторон прямоугольного треугольника. А точнее, две стороны, которые образуют тот самый прямой угол.

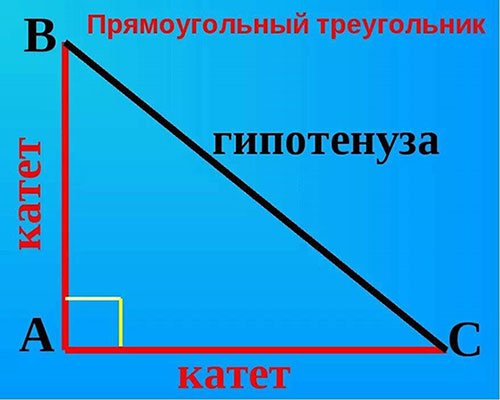
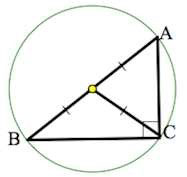
На этом рисунке катеты обозначены точками АВ и АС.

Само слово имеет греческие корни. И в переводе «káthetos» означает «отвесный», «опущенный». Этот термин часто использовали в древнегреческой архитектуре. И кстати, в те времена так обозначали именно вертикальную линию, на которую ориентировались при строительстве.

А потому и катетом какое-то время называли только одну сторону прямоугольного треугольника, а именно ту, которая идет вертикально. В нашем случае это сторона АВ. А вот сторона АС называлась «основанием», что собственно выглядит вполне логично, так как именно на этом основание опирается весь треугольник.

Но после решили, что смотреть на фигуру можно под разными углами. А значит, чтобы не возникла путаница, обе стороны стали называть катетами.

Катеты бывают двух видов:

1. прилежащие к какому-то углу;
2. противолежащие от какого-то угла.

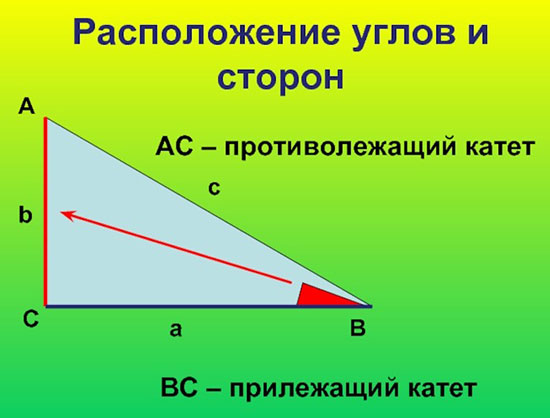
И все зависит от того, о каком конкретно угле идет речь. Например, рассмотрим этот рисунок. Если возьмем угол в точке В, то прилежащим катетом будет сторона ВС, а противолежащим – АС. А если мы рассматриваем угол в точке А, то прилежащим катетом становится сторона АС, а противолежащим – ВС.

Что такое гипотенуза

Гипотенуза – это последняя и самая длинная сторона прямоугольного треугольника. Она расположена напротив прямого угла и соединяет концы обоих катетов.

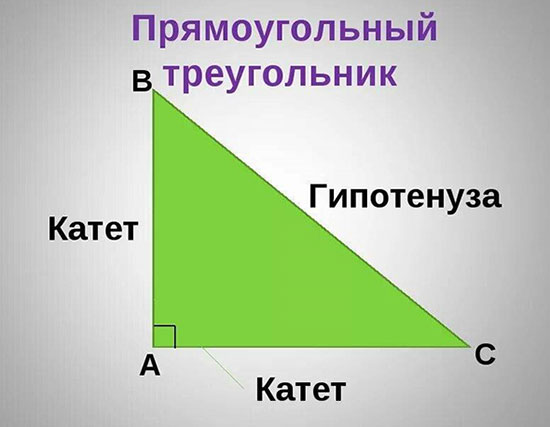
Слово «гипотенуза» также имеет греческие корни. И в переводе «upoteiuosa» означает «натянутая». Почему так? Ответ надо искать даже не в Древней Греции, а еще раньше – в Древнем Египте.

Египтяне были весьма искусны в строительстве. Ярким доказательством этого являются Пирамиды – единственное из чудес света, которое сохранилось до наших дней. А ведь они были возведены более 4,5 тысяч лет назад.

Одним из секретов пирамид является то, что у них точно соблюдены пропорции. И в частности все углы строго прямые.

Причем, оптических измерительных приборов, которые используют сейчас, в те времена не было. Поэтому египтяне придумали уникальную технологию:

1. Они не размечали сразу квадратное или прямоугольное основание, так как был серьезный риск, что противоположные стороны перекосятся. И получится в лучшем случае трапеция, а в худшем — совсем кривая фигура.
2. Решено было делить фундамент на два прямоугольных треугольника.
3. Чтобы получить точный прямой угол, использовали три веревки. Одна была разделена на три одинаковых отрезка, другая на 4, а третья на 5. Эти цифры в Древнем Египте считались священными, как и 12 – сумму, которую они давали. Но самое главное если три веревки соединить между собой в форме треугольника, то получится идеальный угол в 90 градусов.
4. А дальше они просто брали веревки, которые заранее размечены на 3,4 и 5 одинаковых делений. И с помощью колышков закрепляли их так, чтобы они были натянутыми. С помощью таких нехитрых манипуляций удавалось получить идеальный прямой угол.

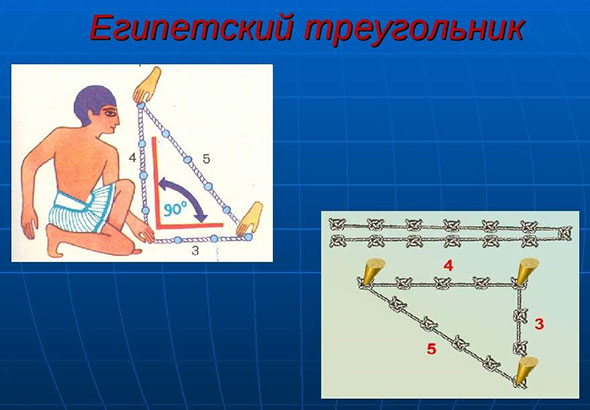
Этот метод до сих пор называют «египетским треугольником». И он настолько точный, что его с легкостью можно использовать и в современном строительстве.

Кстати, необязательно брать конкретно цифры 3, 4 и 5. Главное, чтобы были соблюдены пропорции. Например, их можно умножить на 2 – получится тогда 6, 8 и 10. Или наоборот, поделить на 2 – выйдет 1,5, 2 и 2,5. И так можно менять как угодно. Если соблюдено основное условие, то угол всегда получится идеально прямым.

Ну, а если вернуться термину «гипотенуза», то теперь легко объяснить, почему эту линию называли «натянутой».

Свойства и признаки прямоугольных треугольников

Если у прямоугольного треугольника катеты имеют равную длину, то он называется равнобедренным. Соответственно, и острые углы у него будут равны.

Признаки равенства треугольников

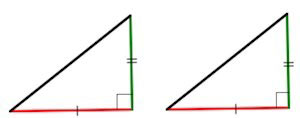
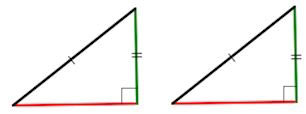
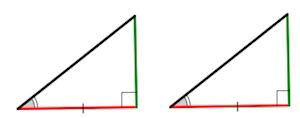
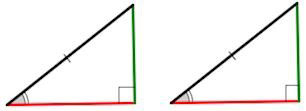
Также по катетам, гипотенузе и углам можно доказать, что два треугольника равны между собой. Есть разные методы:

1. По двум катетам
   
2. По гипотенузе и одному из катетов
   
3. По острому углу и прилегающему к нему катету
   
4. По гипотенузе и острому углу
   

Свойства треугольников

С гипотенузой и катетами связаны и определенные свойства прямоугольных треугольников:

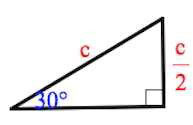
1. Если у треугольника острый угол равен 30 градусам, то длина противоположного к нему катета равна половине гипотенузы. Это правило действует и в обратном порядке – если катет вдвое меньше гипотенузы, то противоположный угол равен 30 градусам.
   
2. Если знать длину обоих катетов, то можно легко вычислить площадь треугольника. Для этого есть формула, в которой

   S = (A * B) / 2

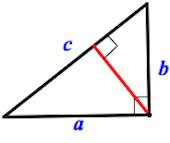
   где S – площадь, А и В – длины катетов.
3. Высота, проведенная из прямого угла к гипотенузе, вычисляется по формуле

   H = A * B / C

   где А и В – длины катетов, С – длина гипотенузы.

   
4. Если вокруг прямоугольного треугольника описать окружность, то ее центр будет совпадать с серединой гипотенузы.
   

Тригонометрические функции

На значениях катетов и гипотенузы строится целый раздел математики, который называется тригонометрией.

В нем 4 основных функции:

1. Синус – отношение противоположного катета к гипотенузе;
2. Косинус – отношение прилегающего катета к гипотенузе;
3. Тангенс – отношение противоположного катета к прилегающему;
4. Котангенс – отношение прилегающего катета к противоположному.

Эти величины используются не только в геометрии. Они имеют большое значения для физики, архитектуре и астрономии. В частности, с их помощью контролируют движение космических спутников.

Теорема Пифагора

Эта теорема является самой известной в геометрии. И известна она была, кстати, еще задолго до рождения знаменитого греческого математика. Мы уже говорили, что древние египтяне с успехом пользовались треугольником со сторонами 3:4:5. Кстати, по таким же принципам строили и в Вавилоне, и в Китае. А это было за несколько тысяч лет до того, как Пифагор появился на свет.

Тогда почему же эта теорема названа его именем? Все просто – он математически доказал то, что другие до него просто использовали.

История Пифагора достаточно интересна. В 22 года он отправился в египетский Мемфис, где несколько лет изучал геометрию. Именно там он узнал про «магическое» соотношение сторон прямоугольного треугольника. А когда возвращался на родину, попал в плен к царю Вавилона. И находясь в Месопотамии, также активно изучал математику.

Все это и позволило ему в итоге озвучить и доказать свою теорему. Звучала она изначально так:

«Квадрат стороны, которая лежит напротив прямого угла, равен сумме квадратов сторон, которые к нему прилегают»

Ну в наше время ее формулируют еще проще:

«Сумма квадратов катетов равна квадрату гипотенузы»

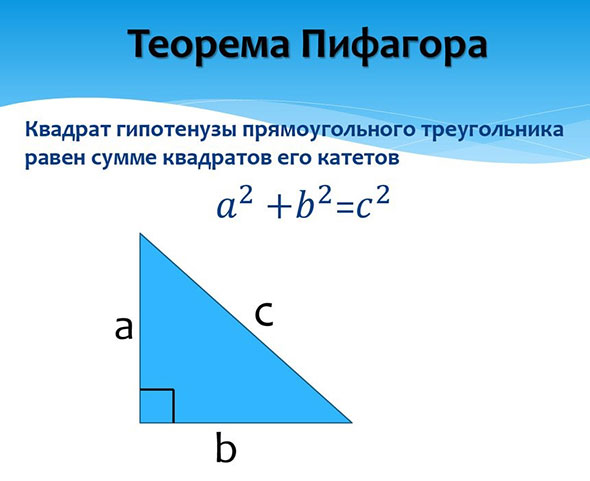
Интересно, что документально доказательство теоремы Пифагор нигде не оставил. Или эти бумаги просто не дожили до наших дней. О том, что именно он это сделал, на страницах своих книг говорит другой известный математик – Евклид.

Кстати, сегодня существует более 400 различных доказательств теоремы Пифагора. По этому показателю она даже занесена в книгу рекордов Гиннесса.