Что такое окружность и какова ее формула
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Есть два геометрических понятия, которые встречаются в абсолютно любой области человеческой деятельности.
Одна из них – прямая, а вторая – окружность. И о ней мы более подробно поговорим в этой статье.
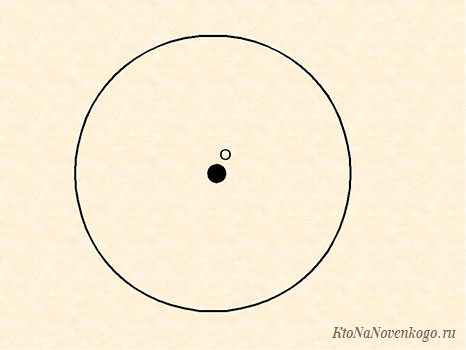
Окружность — это...
Окружность — это множество всех точек на плоскости, находящихся на одинаковом расстоянии от данной точки. Радиус окружности — отрезок, соединяющий любую её точку с центром. Все радиусы окружности равны. Хорда окружности — отрезок, соединяющий две любые её точки. Диаметр окружности — это хорда, которая проходит через центр окружности.
Окружность действительно является одной из базовых составляющих не только науки, но и нашей повседневной жизни. Мы едем в транспорте, у которого круглые колеса. Мы едим из тарелок и пьем из кружек, которые также имеют форму окружности.
Да даже все планеты нашей Солнечной системы круглые, и движутся они по окружности.
С самим понятием окружности каждый из нас сталкивается еще в начальной школе. Вот как выглядит определение из учебников математики:
Окружность – это кривая, которая состоит из множества точек, равноудаленных от одной заданной точки.
В данном примере той точкой, от которой равноудалены все остальные, является точка О (см. рисунок выше). И официально она называется центром окружности.
Впервые окружности и все, что с ними связано, были описаны в Древней Греции. В книге «Начала» знаменитого математика Евклида. Этой теме он посвятил всю третью часть своего произведения.
Радиус и диаметр окружности
Чтобы начертить окружность, нужен специальный инструмент. Сделать это от руки не получится. Даже если человек будет максимально аккуратен, все равно линия получится неидеальной. Поэтому не обойтись без циркуля.
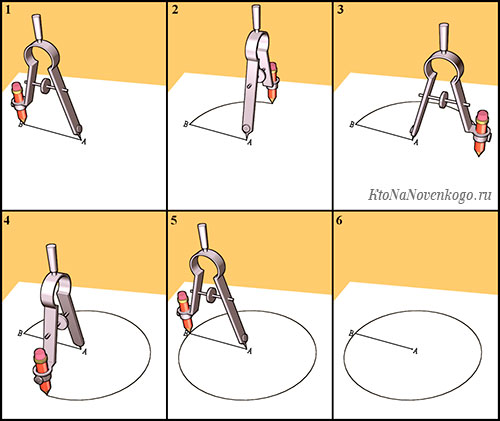
Пользоваться им просто. Одна ножка с острым концом устанавливается в центре будущей окружности. А вторая с грифелем чертит вокруг центра ровную окружность. А вот расстояние между ними, которое на данном рисунке обозначено AB, называется радиусом.
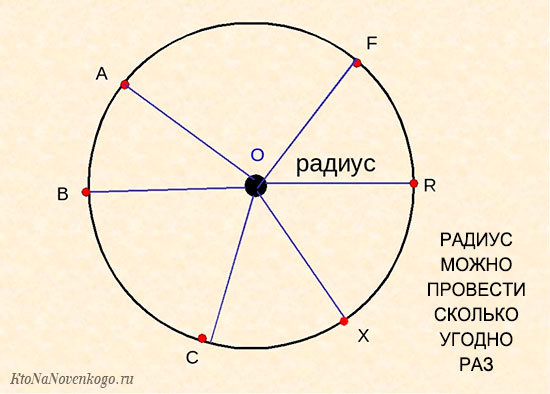
Радиус окружности – отрезок, который соединяет центр окружности с любой точкой на ее поверхности.
Обозначается радиус всегда латинской буквой «R» или «r». Количество радиусов для любой окружности бесконечно.
А второе базовое понятие для любой окружности – диаметр.
Диаметр – отрезок, который соединяет две противоположные точки на поверхности окружности, и при этом обязательно проходит через ее центр.
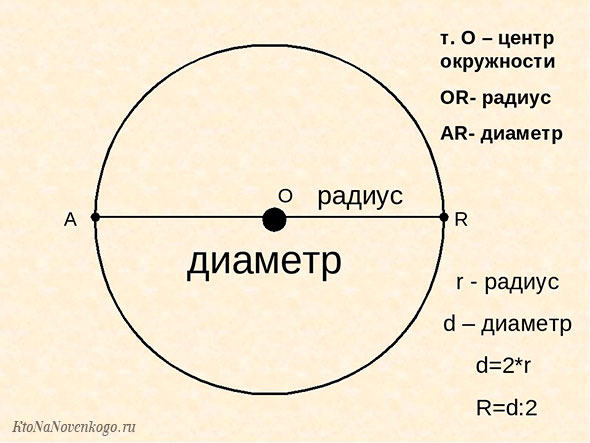
Обозначается диаметр другой латинской буквой – «D» или «d». Как видно из этого рисунка, диаметр равен сумме двух радиусов. И эта формула известна каждому школьнику.
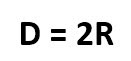
Окружность, у которой радиус равен 1, принято называть единичной. С ней связано очень много понятий в тригонометрии. А вот окружность с нулевым радиусом, является обычной точкой.
Формула окружности
И еще два базовых понятия, которые связаны с окружностью.
Для вычисления длины окружности используется формула:
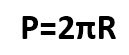
А для вычисления площади круга:
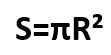

И в данных формулах наибольший интерес представляет буква «π», которая называется числом «пи» и является математической постоянной. А равна она 3,14.
Хотя на самом деле количество знаков после запятой бесконечно, но для упрощения принято использовать только до сотых значений. Более подробно о числе «пи» вы можете прочитать в отдельной статье.
Комментарии и отзывы (2)
Если радиус равен нулю, то это либо не окружность, либо ничто. Можно ли сказать, что точка — это окружность? Если да, то её радиус должен быть отличен от нуля, хоть и очень мал.
Кстати начертить можно и без специального инструмента. Можно просто с помощью нитки и карандаша или ручки. Привязываете один конец к гвоздику например, и это будет центр окружности. А к другому концу нитки — ручку. И получится идеальный круг.
Можно отмерить нитку той длины, которая нужна и будет нужный размер круга.
Ваш комментарий или отзыв