Хорда — это геометрическая струна

Слово это имеет древнегреческие корни и переводится как «струна».

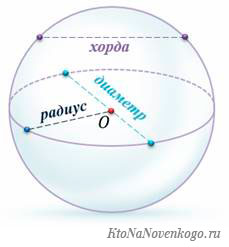
Это очень точно характеризует ее внешний вид, так как хорда представляет собой прямую линию.

Хорда — это...

Термин этот применяется сразу в нескольких областях:

1. В геометрии хорда – это часть прямой, которая проходит между двумя точками на окружности или эллипсе;

2. В биологии – скелетная позвоночная ось у всех животных, включая человека;
3. В авиации хорда – это расстояние между двумя наиболее удаленными точками на крыле любого летательного аппарата;
4. В медицине и анатомии – нервные волокна, которые соединяют стенки желудочков сердца и края желудочковой стороны створок клапанов (трехстворчатого и митрального);
5. В ботанике хорда – это разновидность бурых водорослей, которая бывает двух видов – пушистая и нитевидная.

Но в рамках этой статьи мы подробно рассмотрим первый вариант значения термина ХОРДА. Тот, который применяют в геометрии, и который школьники подробно изучают в 7 классе.

Что такое хорда в геометрии

Хорда – это отрезок прямой, которая проходит через две точки на любой кривой линии. Это могут быть окружность, эллипс, гипербола или парабола.

Выглядит она вот так:

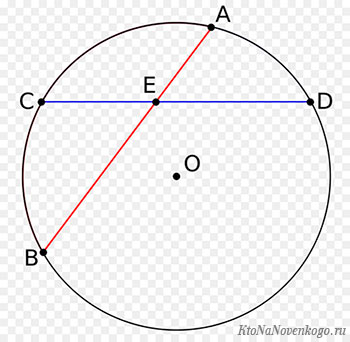
На этом рисунке изображены сразу две хорды – AB и CD. А есть еще частный случай, когда хорда проходит через центр окружности.

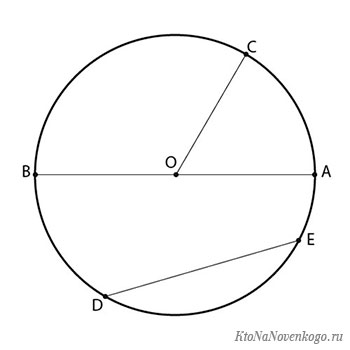
На данном рисунке это отрезок AB, будет являться диаметром окружности. И как нетрудно догадаться, это самая длинная хорда, которая может быть для данного примера.

Свойства хорды

Если сравнивать ее с другими частями окружности, то можно вывести целый ряд закономерностей.

Например, хорда и радиус:

1. Если радиус поделил хорду пополам, то оба отрезка перпендикулярны друг другу. И наоборот – если хорда и радиус перпендикулярны, то радиус поделит хорду на две равные части.
2. Если радиус поделил хорду на две равные половины, то он точно так же поделит на равные части и дугу окружности, которая «стягивает» эту хорду. Аналогично правдиво и обратное утверждение – если пополам делится дуга окружности, то пополам будет делиться и хорда.
3. И наконец, объединяя первые два пункта. Если радиус может поделить дугу пополам, то он пересекает хорду под прямым углом.

Хорда и диаметр:

1. Если диаметр разделяет хорду на две равные части, то они перпендикулярны друг другу. Верно и противоположное утверждение.
2. Если диаметр разделяет пополам хорду, то точно так же делится и дуга, образованная этой хордой. Верно и обратное свойство.
3. Если диаметр и хорда пересекаются под прямым углом, то он делит ее дугу пополам. Точно так же и в обратном случае.

Хорда и центр окружности:

1. Если две или несколько хорд равны между собой, то они находятся на одном расстоянии до центра окружности. Верна и обратная зависимость между расстоянием от центра и длиной хорд.
2. Чем длиннее хорда, тем ближе она находится к центру фигуры. И чем она короче, тем дальше она от центра и ближе к дуге.
3. Если у хорды максимально возможная длина, то она является диаметром. А если наименьшая, то речь идет о точке.

И еще одно свойство. Если взять уже знакомый нам рисунок расположенный сразу под определением, то при пересечении хорд получается вот такая зависимость – произведение частей одной хорды равна произведению частей другой:

AE * EB = CE * ED

Как рассчитать ее длину

Длина хорды – это расстояние от одной точки пересечения с окружностью до другой. Чаще всего она обозначается латинской буквой «L».

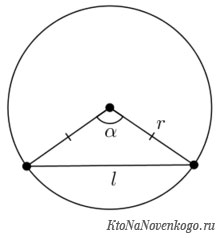
Чтобы рассчитать длину хорды, надо знать значение радиуса и центрального угла. Формула выглядит так:

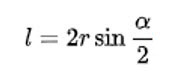
Вот и все, что мы хотели рассказать о ХОРДЕ.