Что такое рациональные числа

И на этот раз расскажем все о РАЦИОНАЛЬНЫХ ЧИСЛАХ. Они обязательно входят в школьную программу, и дети начинают изучать их в 6 классе.

Само слово «рациональный» знакомо многим. И под ним подразумевается нечто «логичное» и «правильное». На деле так и есть.

Рациональные числа — это ...

Термин имеет латинские корни, и в переводе «ratio» означает «число», «расчет», «разум», «рассуждение» и «нумерация». Но есть и другие переводы – «дробь» и «деление».

РАЦИОНАЛЬНОЕ ЧИСЛО – любое число, которое можно показать в виде дроби a/b. Здесь а – целое число, а b – натуральное.

Стоит напомнить, что:

1. Целые числа – это все возможные числа, как отрицательные, так и положительные. И к ним же относится ноль. Главное условие – они не должны быть дробными. То есть -15, 0 и +256 можно назвать целыми числами, а 2,5 или -3,78 – нет.
2. Натуральные числа – это числа, которые используются при счете, то есть они имеют «натуральное происхождение». Это ряд из 1, 2, 3, 4, 5 и так далее до бесконечности. А вот ноль и отрицательные числа, как и дробные – к натуральным не относятся.

И если применить эти определения, то мы можем сказать, что:

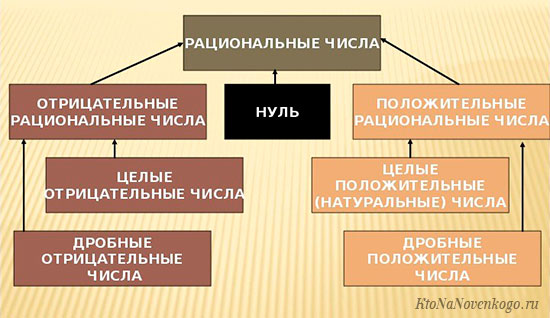
РАЦИОНАЛЬНОЕ ЧИСЛО – это вообще все возможные числа, кроме бесконечных непериодических десятичных дробей. Среди них натуральные и целые числа, обыкновенные и конечные десятичные дроби, а также бесконечные периодические дроби.

История изучения рациональных чисел

Точно неизвестно, когда люди начали изучать дроби. Есть мнение, что много тысяч лет назад. И началось все с банального дележа. Например, кому-то нужно было разделить добычу, но на равные части это не получалось сделать. Зато получалось сколько-то целых, и сколько-то в довесок.

Скорее всего, дроби изучали и в Древнем Египте, и в Древней Греции. Тогдашние математики далеко продвинулись в науке. И трудно предположить, что эта тема осталась ими не изучена. Хотя, к сожалению, ни в одних трудах так и не было найдено конкретных указаний на рациональные числа.

А вот официально считается, что понятие десятичной дроби появилось в Европе в 1585 году. Этот математический термин в своих трудах увековечил голландский инженер и математик Симон Стевин.

До занятия наукой, он был обыкновенным купцом. И скорее всего, именно в торговых делах часто сталкивался с дробными числами. Что потом и описал в своей книге «Десятая».

В ней Стевин не только объяснял полезность десятичных дробей, но и всячески пропагандировал их использование. Например, в системе мер для точного определения величины чего-либо.

Разновидности рациональных чисел

Мы уже написали, что под понятия рациональные числа подпадают практически все возможные варианты. Теперь рассмотрим более подробно существующие варианты:

1. Натуральные числа. Любое число с 1 и до бесконечности можно представить в виде дроби. Достаточно вспомнить простое математическое правило. Если поделить число на единицу, то получится то же самое число. Например, 5 = 5/1, 27 = 27/1, 136 = 136/1 и так далее.
2. Целые числа. Точно такая же логика, как в случае с натуральными числами, действует и тут. Отрицательные числа также можно представить в виде дроби с делением на единицу. И точно также будет в отношении нуля. Например, -356 = -356/1, -3 = -3/1, 0 = 0/1 и так далее.
3. Обыкновенные дроби. Это напрямую говорится в определении рациональных чисел. Например, 6/11, 2/5, -3/10 и так далее.
4. Бесконечные периодические дроби. Это числа, у которых после запятой бесконечное множество знаков и их последовательность повторяется. Самые простые примеры 1/3, 5/6 и так далее.
5. Конечные десятичные дроби. Это числа, которые можно записать двумя разными вариантами, и у которых вполне конкретное количество знаков после запятой. Самый простой пример – половина. Ее можно обозначить дробью 0,5 или дробью ½.

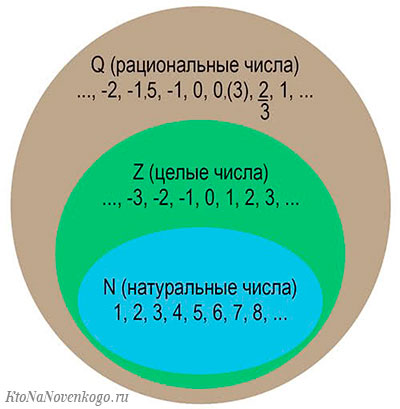
Все числа, которые входят в понятие рациональных, называются МНОЖЕСТВОМ рациональных чисел. В математике его принято обозначать латинской буквой Q.

А графически это можно изобразить вот так:

Свойства рациональных чисел

Рациональные числа подчиняются всем главным законам математики:

1. А + В = В + А
2. А + (В + С) = (А + В) + С
3. А + 0 = А
4. А + (-А) = 0
5. А * В = В * А
6. А * 1 = А
7. А * 0 = 0
8. (А + В) * С = А * С + В * С
9. (А – В) * С = А * С – В * С

Ради интереса можете попробовать подставить вместо букв любые числа и убедиться, что эти законы верны.

Вместо заключения

Раз есть в математике рациональные числа, значит, должны быть и им противоположные. Так и есть – они называются иррациональными. Это числа, которые нельзя записать в виде обычной дроби.

К таким числам относится математическая константа «пи». Многие знают, что она равна 3,14 и бесконечное количество знаков после запятой, причем их последовательность никогда не повторяется.

Также к иррациональным числам относится много корней. Это касается тех, у кого в результате не получается целого числа. Самый простой пример – корень из 2. Но это уже тема для другой статьи.