Простые числа — это чудеса деления

В школе это проходят в 5 или 6 классе, в зависимости от программы обучения.

И интересно, что если спросить школьников, что такое простые числа, то они, скорее всего, ответят правильно.

А вот взрослые задумаются и не факт, что вспомнят точное определение. Так что это статья скорее для них.

Простые числа — это...

Итак, вот как выглядит официальное определение:

Простые числа – это такие числа, которые имеют только два делителя. Один из них – единица, а другое – само число.

Чтобы было более понятно, приведем простой пример. Для чисел 5 и 7 надо найти все возможные делители, чтобы в результате образовалось целое число.

Если вы попробуете решить эту задачку, то получите, что 5 и 7 делятся только на 1 и 5, и 1 и 7 соответственно. Во всех других случаях вы получите дробное число. И это как раз означает, что числа 5 и 7 относятся к простым.

А вот попробуем по той же схеме разобрать числа 6 и 9. В первом случае мы получим, что 6 можно поделить на 1, 2, 3 и 6, а число 9 – на 1, 3 и 9. И это уже противоречит определению простых чисел, значит, 6 и 9 таковыми не являются.

Они называются в математике – СОСТАВНЫМИ ЧИСЛАМИ.

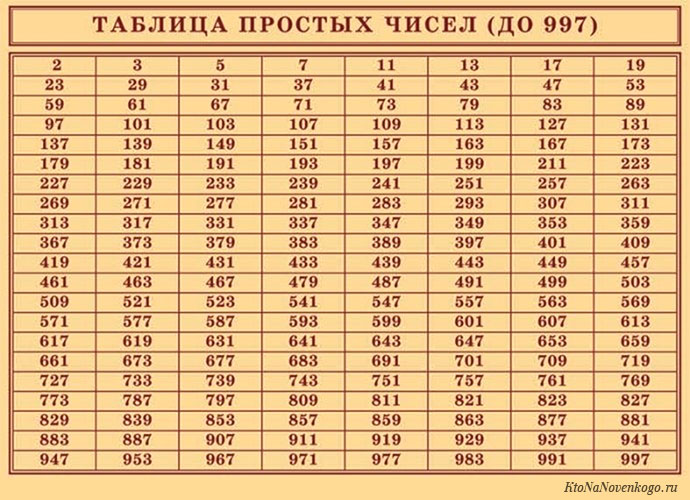
Список и таблица простых чисел

Некоторые ошибочно полагают, что наименьшее простое число – это единица.

С одной стороны, в этом есть логика, так как 1 делится только на 1. Но это получается одно и то же число (единица), что противоречит определению простых чисел, в котором четко прописано – «делителей должно быть два».

Значит, минимальное простое число – это 2. А первоначальный ряд выглядит следующим образом:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199…

При желании можете проверить эти числа на предмет деления. Мы же скажем, что этот ряд на самом деле не окончательный.

Количество простых чисел не ограничено. Или говоря математическим языком, оно стремится к бесконечности.

История простых чисел

Первые упоминания о простых числах относятся к Древнему Египту. В Британском музее хранится папирус, который датируется 2000 годом до нашей эры. И на нем, согласно расшифровке, содержится учебное пособие по арифметике.

В том числе и про деление чисел. Называется этот артефакт – папирус Райнда, по имени его первого владельца.

В этом документе есть таблица, в которой указаны числа, делящиеся на различные знаменатели. Причем они разделены таким образом, что становится понятно – древние египтяне может и не пользовались понятиям «простое число», но хотя бы имели о нем представление.

Ну а первые исследования простых чисел датируются 300 годом до нашей эры. И связаны они с именем знаменитого древнегреческого математика Евклида.

Как и многое другое, он описал простые и составные числа в своем известном произведении «Начала».

В частности, Евклид описал такие вещи, как:

1. Основная теорема арифметики;
2. Бесконечность прямых чисел;
3. Лемма Евклида.

Сейчас расскажем об этих понятиях подробнее.

Основная теорема арифметики

Основная теорема арифметики, которую придумал еще Евклид, гласит:

Любое натуральное число, которое больше единицы, может быть представлено в виде произведения простых чисел. Причем их количество не ограничено, а порядок следования неважен.

Если обозначить исходное число буквой N, а простые числа буквами Р1, Р2, Р3 и так далее, то можно записать эту теорему следующим образом:

N = Р1 * Р2 * Р3 * … * РК

Например, возьмем число 100. Его можно разложить на следующие простые числа:

100 = 5 * 5 * 2 * 2

Или более сложный пример – число 23244:

23244 = 149 * 13 * 3 * 2 * 2

Раскладывать на простые числа легко. Можно сперва делить на 2 и 3, а уже в конце автоматически получить более сложные делители.

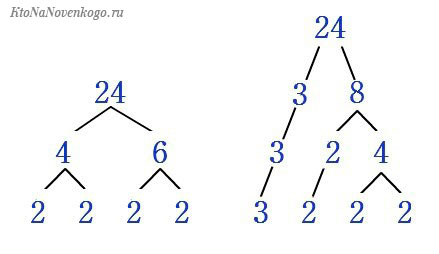
Ради интереса придумайте любое число и сами найдите его составляющие.

Лемма Евклида

Еще одна теорема, которая имеет прямое отношение к простым числам. Она гласит;

Если некое простое число Р делит произведение чисел X и Y без остатка, то оно может точно так же поделить или X, или Y.

Звучит несколько сложновато, хотя на деле все это просто. Так, возьмем для примера P = 2, X = 6, Y = 9. И тогда получается, что

X * Y = 6 * 9 = 54

В нашем примере P делит это произведение без остатка:

(X * Y) / P = 54/2 = 27

А значит наша P может поделить без остатка или X, или Y. Очевидно, что это X:

X/P = 6/2 = 3

Y/P = 9/2 = 4,5 (не подходит)

Как быстро и легко определить простые числа

И еще одно понятие, которое связано с простыми числами. Оно названо в честь другого древнегреческого математика Эратосфена Киренского.

Этот человек придумал, как быстро и легко определить простые числа. В частности, он сделал таблицу, в которой были указаны значения до 1000.

Свою таблицу он нарисовал на глиняной дощечке. А после прокалывал те клеточки, на которых были написаны составные числа. В результате получилось нечто вроде решета, отсюда собственно и название метода.

Кстати, пользоваться решетом Эратосфена весьма просто. Например, сделаем таблицу до 50.

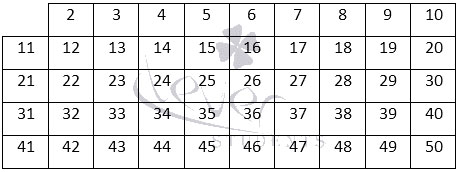
После этого из нее надо поочередно вычеркивать числа, которые кратны 2, 3, 5, 7 и 11. В результате получится вот это:

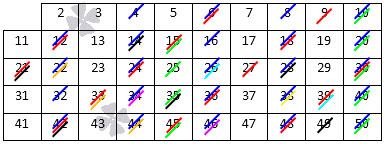
Те числа, которые остались, и есть простые. Можете сравнить этот ряд с тем, который мы давали в начале статьи. Точно таким же способом можно составить абсолютно любой ряд простых чисел = хоть до тысячи, хоть до миллиона и больше.